ENEM 2017) - QUESTÃO

A técnica do carbono-14 permite a datação de fósseis pela medição dos valores de emissão beta desse isótopo presente no fóssil. Para um ser em vida, o máximo são 15 emissões beta/(min g). Após a morte, a quantidade de 14C se reduz pela metade a cada 5730 anos.

A prova do carbono 14.Disponível em: http://noticias.terra.com.br. Acesso em: 9 nov. 2013 (adaptado).

Considere que um fragmento fóssil de massa igual a 30 g foi encontrado em um sítio arqueológico, e a medição de radiação apresentou 6750 emissões beta por hora. A idade desse fóssil, em anos, é

a) 450.

b) 1433.

c) 11460.

d) 17190.

e) 27000.

_______________________________________________________________
➥ Resposta comentada: (c)

Cálculo do número de emissões beta inicial:

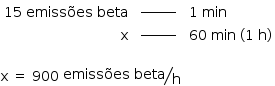
Para um fragmento fóssil de 30 g, tem-se:

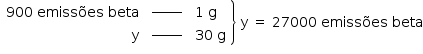
Cálculo da idade do fóssil

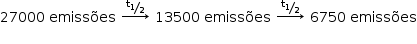
2 meias-vidas = 2 × 5730 = 11460 anos